접근 방식
문제에서 바위 n개를 제거했을 때, 각 바위 사이의 거리가 최소인 값들 중 최댓값을 구하라고 합니다.
즉, 각 바위 사이의 거리가 최소인 값들에 대해 알아야 합니다.
어떻게 각 바위 사이의 거리가 최소인 값을 알 수 있을까요?
(1) 브루트 포스
맨처음 제가 생각했던 방식은 단순한 조합을 사용해서 n개의 조합을 전부 확인해 바위 사이의 거리가 최소인 값을 하나의 리스트에 담아 정렬을 한 후, 제일 큰 값을 도출해야겠다고 생각했습니다. 문제에서 주어진 조건은 아래와 같습니다.

바위의 갯수가 최대 50,000개 이므로 제거할 바위의 조합의 시간복잡도는 50,000Cn이 됩니다.
최악의 경우 O(50,000^n) 에 가깝게 증가합니다. n이 2만되도 시간 초과가 발생할 것 같아서 스킵합니다.
(2) 투포인터 알고리즘
만약 2개로 제한이 되어있었다면, O(N)이 걸리는 투포인터 알고리즘을 사용하려고 했습니다. 하지만, 문제는 N개를 골라야 하므로 투포인터로 접근하는 방법은 스킵합니다.
(3) 이분 탐색
마지막으로 이분 탐색을 고려해 보았습니다. 이분 탐색은 특정 값을 찾기 위한 알고리즘으로, 시간 복잡도가 O(log N)으로 매우 효율적입니다.(최후의 수단이라고 생각을 해서 선택을 했습니다.)
이분 탐색 알고리즘을 사용하기로 선택했고, 문제에 어떻게 접근을 해야할까요?
이분 탐색으로 찾으려는 값을 정해야 합니다. 문제는 각 바위 사이의 거리가 최소인 값들 중 최댓값을 구하라고 합니다.
즉, 각 바위 사이의 거리가 최소인 값을 타겟으로 두었습니다.
이분탐색의 필수조건은 정렬이 된 배열에서만 가능하다는 것입니다. 그렇기에 먼저 rocks의 배열을 정렬해 주었습니다.
각 바위 사이의 거리가 최소인 값을 찾기 위해 먼저 각 바위 사이의 거리가 최소인 값과 최대인 값을 양 끝쪽 값으로 설정해주었습니다.
또한, 각 바위 사이의 거리가 최소라는 말은, 모든 바위 간의 거리가 해당 최소 거리 이상이어야 한다는 뜻입니다.
해당 최소 거리 이상이라는 것을 어떻게 판단할까요?
반복문을 사용하여 매번 바위 사이의 거리를 갱신하면서, 해당 거리보다 작은 바위 간의 거리 개수를 카운트합니다.
이 과정은 최대 n개의 바위를 제거할 수 있기 때문에, 현재 제거해야 할 바위 개수를 확인하여 n과 비교하기 위해 수행됩니다.
- 만약 카운트한 개수가 n보다 크다면, 제거해야 할 바위가 너무 많다는 의미이므로 각 바위 사이의 최소 거리를 줄여야 합니다.
- 반대로, 카운트한 개수가 n 이하라면, 더 큰 거리에서도 조건을 만족할 수 있으므로 각 바위 사이의 최소 거리를 늘려도 됩니다.
이 과정을 반복하면 최종적으로 가능한 최소 거리 중 최댓값을 구할 수 있습니다.
하나의 예시를 통해서 이 방법이 옳은지 판단해보겠습니다.
접근 방식 증명
하나의 예시는 아래와 같습니다.
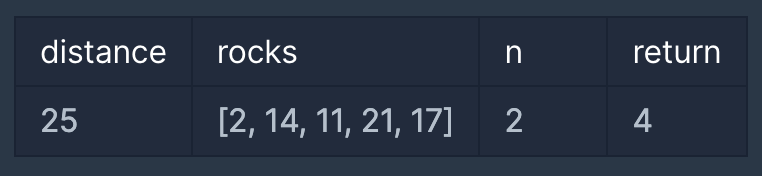
먼저, rocks를 정렬합니다.
[2, 11, 14, 17, 21]

각 돌 사이의 최소 거리는 돌이 총 n개가 제거될 수 있기 때문에 1부터 25까지 가능합니다.
아래 과정에서 mid가 의미하는 것은 각 바위 간의 거리를 의미합니다.
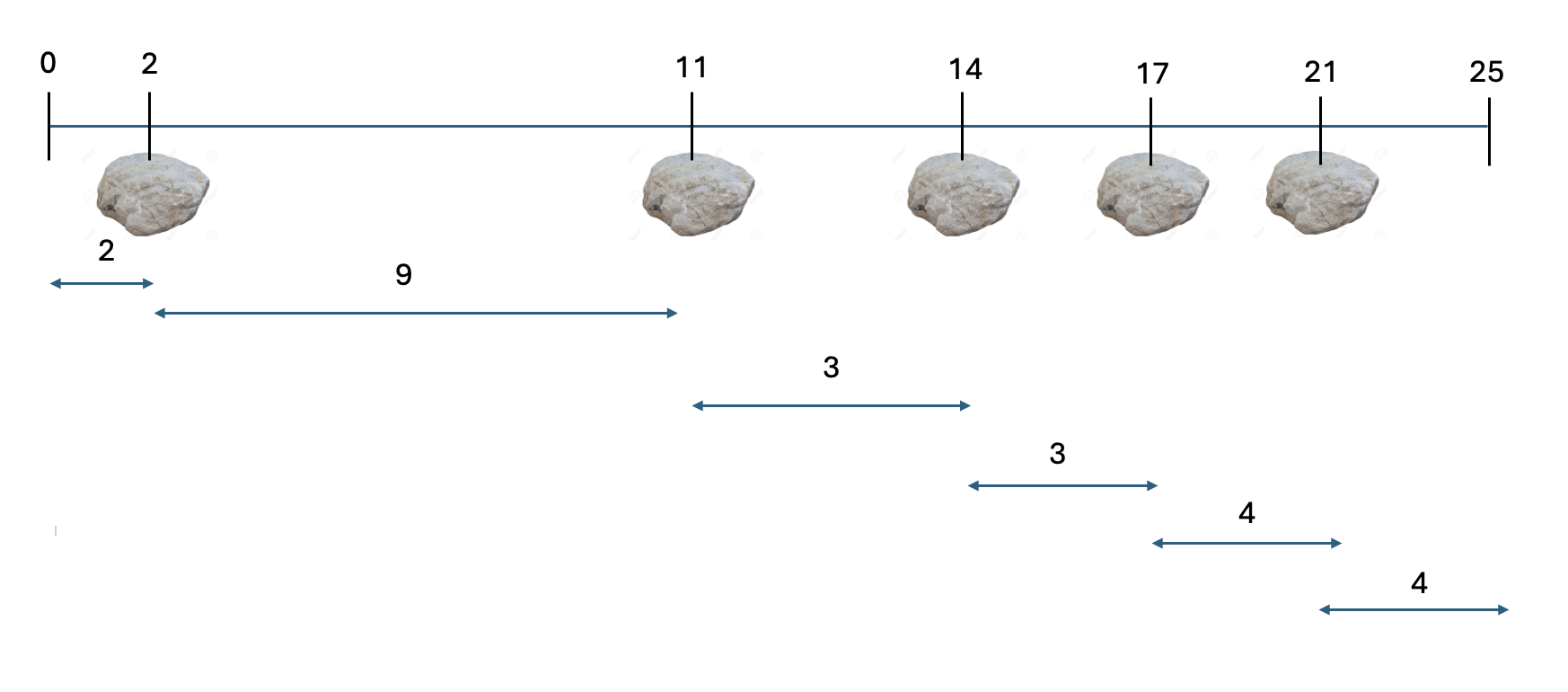
(1) start = 1, end = 25, mid = (1+25) / 2
mid가 13일땐, 모든 바위 사이의 거리가 13보다 작게 나옵니다. 따라서 제거해야하는 바위의 갯수가 2개보다 큽니다.
따라서, 모든 바위 사이의 거리의 값을 더 줄여줍니다.
end = mid - 1을 해줍니다.
(2) start = 1, end = 12, mid = (1 + 12) / 2
mid가 6일땐, (2,11)을 제외한 모든 바위 사이의 거리가 6보다 작게 나옵니다. 따라서 제거해야하는 바위의 갯수가 3개이므로, 2개보다 큽니다.
아래 이미지에서 제거해준 바위는 2,14,21 입니다.
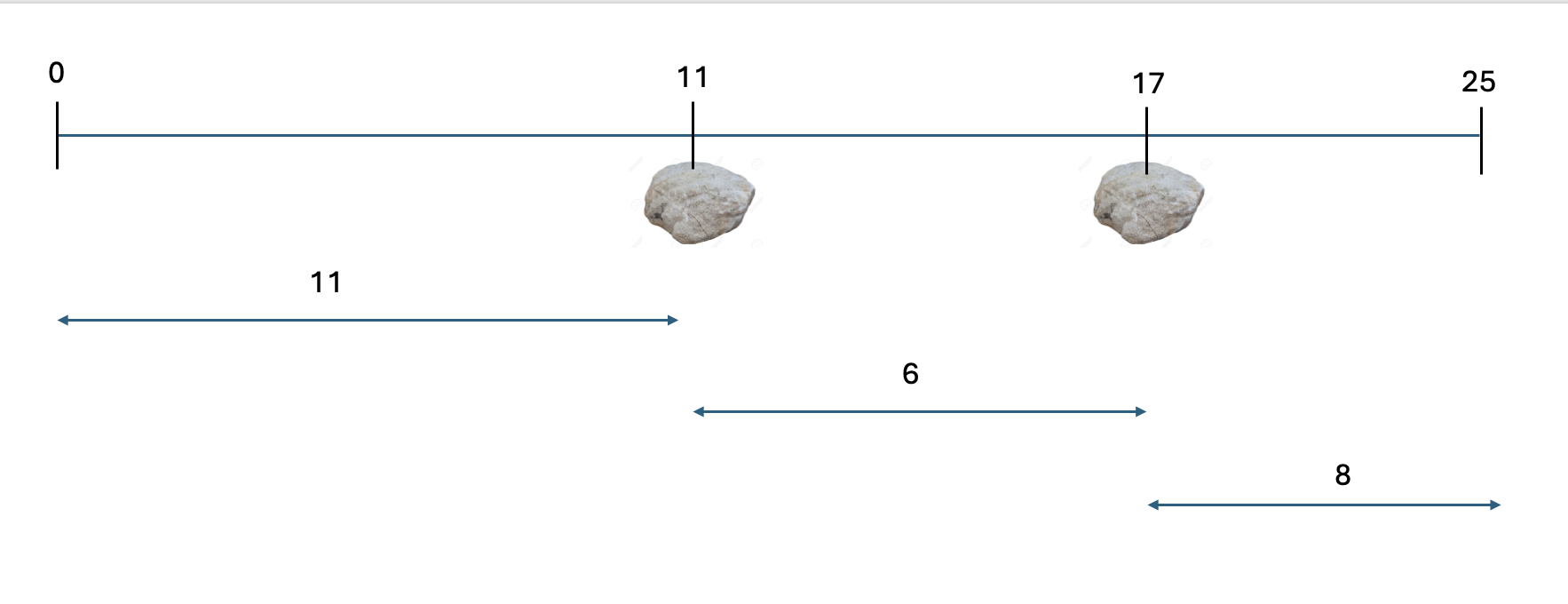
따라서, 모든 바위 사이의 거리의 값을 더 줄여줍니다.
end = mid - 1을 해줍니다.
(3) start = 1, end = 5, mid = ( 1 + 5 ) / 2
mid가 3일 때, (0,2) 구간만 바위 사이의 거리가 3보다 작아 제거 대상이 됩니다.
이때, 제거해야 하는 바위의 개수가 1개로 주어진 n = 2보다 작습니다. 이는 아직 바위를 1개 더 제거할 수 있다는 의미이며, 현재 최소 거리(mid = 3)보다 더 큰 값에서도 조건을 만족할 가능성이 있음을 뜻합니다.따라서 돌 사이의 거리를 더 넓은 거리로 늘려도 됩니다.
start = mid + 1을 해줍니다.
(4) start = 4, end = 5, mid = (4 + 5) / 2
mid가 4일때, 구간(0,2), (11,14), (14,17) 구간이 주어진 바위 사이의 거리 4보다 작습니다.
바위 2개 각각 2번과 14번 바위를 제거하면, 주어진 모든 구간이 4보다 커집니다.
두 바위를 제거한 후를 나타내는 이미지는 다음과 같습니다.

제거해야 하는 바위의 갯수가 n=2와 같기 때문에
end = mid - 1을 해줍니다.
(5) start = 4, end = 3
반복문에서 start <= end 라는 조건이 부합하지 않기 때문에, 반복문을 탈출하고 4라는 정답을 도출합니다.
풀이 코드
import java.util.*;
class Solution {
public int solution(int distance, int[] rocks, int n) {
int answer = 0;
Arrays.sort(rocks);
int start = 1;
int end = distance;
while(start <= end) {
int mid = (start + end) / 2;
int removeRockCnt = 0;
int prevRockPosition = 0;
for(int rock: rocks) {
if(rock - prevRockPosition < mid) {
removeRockCnt++;
}else {
prevRockPosition = rock;
}
}
if(distance - prevRockPosition < mid) {
removeRockCnt++;
}
if(removeRockCnt <= n) {
answer = mid;
start = mid + 1;
}else {
end = mid - 1;
}
}
return answer;
}
}
시간 복잡도
배열 정렬 O(NlogN)으로, N은 rocks의 크기를 의미합니다.
Arrays.sort(rocks);
이분 탐색으로 O(logN)으로, N은 distance를 의미합니다.
while(start <= end) {
int mid = (start + end) / 2;
int removeRockCnt = 0;
int prevRockPosition = 0;
for(int rock: rocks) {
if(rock - prevRockPosition < mid) {
removeRockCnt++;
}else {
prevRockPosition = rock;
}
}
if(distance - prevRockPosition < mid) {
removeRockCnt++;
}
if(removeRockCnt <= n) {
answer = mid;
start = mid + 1;
}else {
end = mid - 1;
}
}
출력 결과

'Algorithm' 카테고리의 다른 글
| [프로그래머스] Lv3 선입 선출 (0) | 2025.02.19 |
|---|---|
| [프로그래머스] Lv3 입국심사 (0) | 2025.02.18 |
| [프로그래머스] Lv1 완주하지 못한 선수 (0) | 2025.02.16 |
| [프로그래머스] Lv3 단속 카메라 (0) | 2025.02.15 |
| [프로그래머스] Lv3 섬 연결하기 (0) | 2025.02.14 |



