세그먼트 트리가 뭘까요?
배열을 [0,1,2,3,4]라고 가정합니다.
init() 메서드 과정
public static long init(int start, int end, int node) {
if(start == end) {
return tree[node] = arr[start];
}
int mid = (start + end) / 2;
return tree[node] = init(start, mid, node * 2) + init(mid + 1, end, node * 2 + 1);
}
1. 재귀 호출을 통해서 리프 노드까지 깊이 우선 탐색을 진행합니다.
후위 순회를 통해서 리프 노드에 배열의 값을 저장하고, 부모 노드로 올라가면서 자식 노드들의 합을 구하는 과정입니다.
return tree[node] = init(start, mid, node * 2) + init(mid + 1, end, node * 2 + 1);
리프 노드에 배열에 원소가 채워지고, 왼쪽 자식 노드와 오른쪽 자식노드를 더한 값이 부모 노드가 됩니다.
init() 메서드 흐름
트리 배열이 초기화 되는 과정은 다음과 같습니다.
(무료 GIF 변환 시킨거라 화질이 별로입니다.)
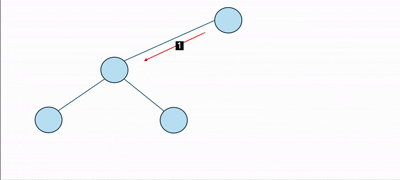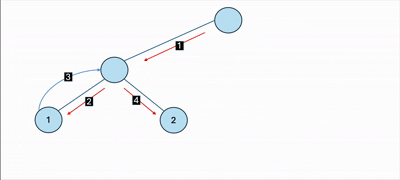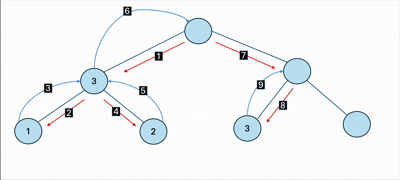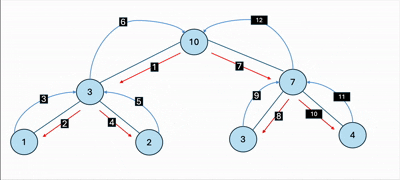
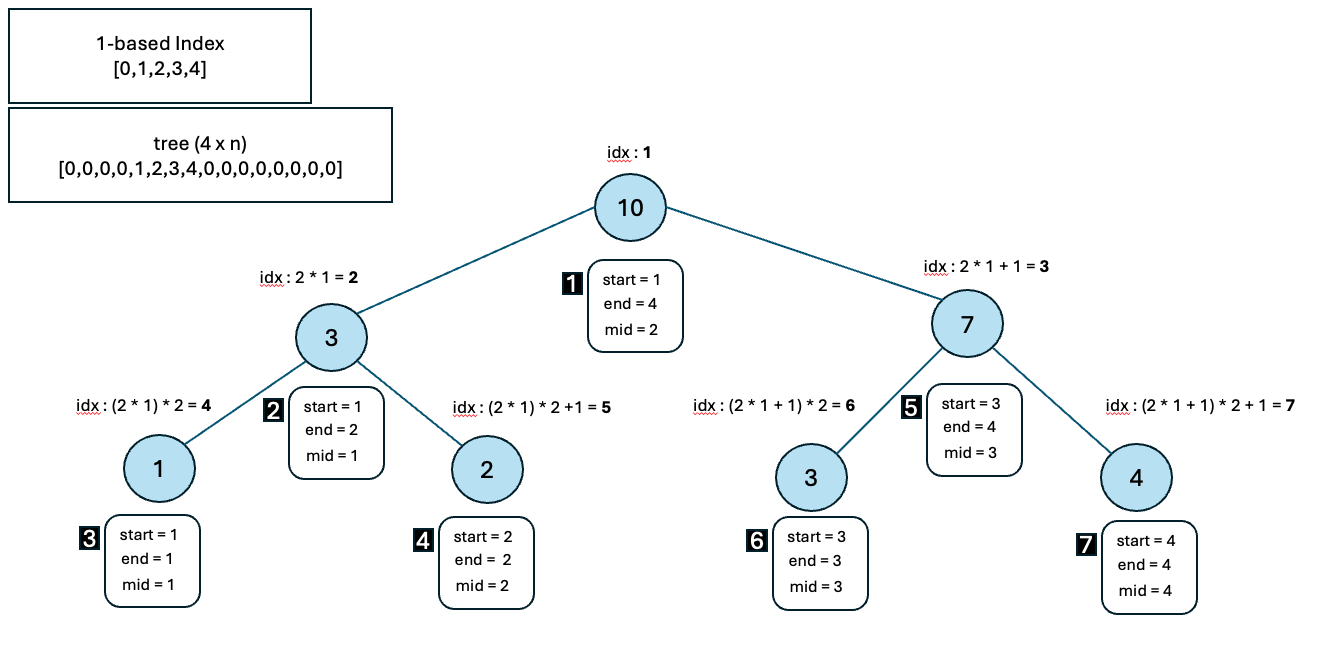
각 노드가 의미하는 값은 뭘까요?
각 노드가 의미하는 값은 특정 구간의 합이 저장되어 있습니다.

이렇게 init() 메서드를 사용해서 특정 구간의 합을 트리의 각 노드에 저장시킵니다.
동적 배열은 배열의 값이 동적으로 변하는 것을 의미합니다.
특정 구간의 합을 트리의 각 노드에 저장 시켰는데, 배열(arr)원소 중 하나가 변경이 되면 어떻게 될까요?
변경된 값이 포함되어 있는 구간합을 다시 갱신해줘야 합니다.
기존 arr배열에서 3번째 값이 5로 변경됬다고 가정해 보겠습니다.
arr = [0, 1, 2, 3, 4] → arr = [0, 1, 2, 5, 4]
값을 갱신하는 과정에 사용되는 메서드는 update() 메서드 입니다.
public static void update(int start, int end, int node, int idx, long dif) {
if(idx < start || idx > end) {
return;
}
tree[node] += dif; // 차이 더해주기
if(start == end) {
return;
}
int mid = (start + end) / 2;
update(start, mid, node * 2, idx, dif); // 리프 노드 탐색
update(mid + 1, end, node * 2 + 1, idx, dif); // 리프 노드 탐색
}
아직 미완성 입니다..!
'Algorithm' 카테고리의 다른 글
| DP (0) | 2025.04.25 |
|---|---|
| [개념 정리] 최단 거리 (0) | 2025.03.12 |
| [개념 정리] DP (0) | 2025.03.11 |
| [개념 정리] 이분 탐색 (0) | 2025.03.10 |
| [프로그래머스] Lv3. 봉인된 주문 (0) | 2025.03.08 |



